

Active power that does real work, is represented on the real axis. Note that the reactive power is represented on the imaginary axis of the diagram. In the power triangle, P is the active power, Q is the reactive power, φ is the phase angle of voltage relative to current, and | S| is the apparent power. However, the wires that provide energy, will become hot (because they are resistive!) and will heat the environment.Īll three power values are pictured in the diagram called the power triangle. So, a purely reactive load will produce no heat itself.

Though this power is called imaginary and wattless, it really heats the grid wires when it goes back and forth over them. It is measured in volt-amperes reactive or vars. Vars: Reactive power, Q is the “imaginary” power in a reactive (capacitive or inductive) load, which represents the exchange of energy between the power source and the reactive load where no power is lost. It is possible, however, just to add the individual VA ratings and the total value will be just an estimate of the total power or current consumed by several devices. Because the majority of loads are non-linear nowadays, there is no straightforward way to obtain an exact total power of several loads by simply adding their currents because they are not in phase with each other (we will talk about it later). Volt-amperes are useful because if the voltage of a device is known, you can calculate the expected maximum current to ensure that the wires and cables supplying this device can withstand it. We will show below that the current in the majority of loads used at home is not sinusoidal - that is why you will need a true RMS digital multimeter. To calculate the apparent power in volt-amperes, you can measure the RMS current and the RMS voltage using a multimeter that can measure the true RMS value of any signal. The apparent power is always higher than the real power because it covers the real and reactive power consumption in the loads. The grid must be built to transport the apparent energy. The RMS calculation includes the effects of all harmonics that are usually present in the current and voltage. It is the product of RMS voltage and current and as such, it is valid regardless of the waveform shape of the voltage and current. Volt-amperes (VA): Apparent power, | S| is the power the electrical grid must be able to withstand.
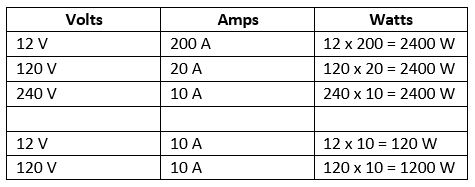
In single-phase AC circuits with pure sinusoidal current, the real power is equal to the product of the RMS current I and voltage U and the cosine of the phase shift between them φ, that isįor non-sinusoidal AC current, the real power is equal to the sum of the corresponding average powers of the individual harmonic components. These measurements are also useful to determine the energy consumed by your devices at home since you pay your utility company for real power. You need to measure the real power, for example, to get rid of the heat generated by the servers in a data center. Real power is usually used for the power rating of resistive loads like ovens and heaters. Ultimately, all real power is converted into heat. It is the rate at which energy is generated or consumed. Watts (W): Real power, P (also called actual power and active power) is the power that actually powers lamps, TVs, computers, and equipment and performs useful work and generates heat. We will also discuss the current waveform distortion in non-linear loads. These values and their calculation are discussed below.
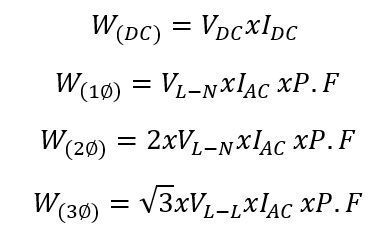
Electrical and electronic products always show one or another power value and sometimes they also show the power factor as well to provide information about the energy they consumed. You can also get the formula used in Watt to Planck Power conversion along with a table representing the entire conversion.Both watts and volt-amperes are units of measurement for electric power. If you encounter any issues to convert, this tool is the answer that gives you the exact conversion of units. Converting Watt to Planck Power is easy, for you only have to select the units first and the value you want to convert. When you are converting power, you need a Watts to Planck Powers converter that is elaborate and still easy to use. helps in the conversion of different units of measurement like W to Planck Power through multiplicative conversion factors. Be it buying grocery or cooking, units play a vital role in our daily life and hence their conversions. Measurement like power finds its use in a number of places right from education to industrial usage. Units of measurement use the International System of Units, better known as SI units, which provide a standard for measuring the physical properties of matter.


 0 kommentar(er)
0 kommentar(er)
